Le coefficient d’aversion au risque

Quand, dans les années 1950, Harry Max Markowitz introduit le concept de « risque » dans un portefeuille, il inaugure en quelque sorte la gestion moderne d’un portefeuille de titres. Son apport a été déterminant pour le développement subséquent des théories modernes de gestion. Le principe fondamental qu’il a lancé est celui de la quantification du risque de rendement d’un portefeuille.

Pour mesurer le risque que présentent les produits financiers par rapport au rendement, on utilise une mesure appelée « écart-type du rendement », communément appelée « volatilité des rendements ». En fait, cette mesure permet de déterminer si le rendement du portefeuille a été uniforme au cours des années ou s’il a subi des variations importantes. Plus le risque a fluctué d’une année à l’autre, plus le rendement espéré est difficile à prévoir; ce portefeuille présente donc un risque plus grand qu’un autre dont le rendement annuel est presque toujours le même.

Markowitz est allé beaucoup plus loin en introduisant le concept de « frontière efficiente ». Par exemple, dans un portefeuille composé de deux titres dont on connaît les rendements et la volatilité, et dans lequel les mouvements de prix de l’un peuvent ne pas influer totalement sur ceux de l’autre, il est possible de calculer le poids de chaque titre pour avoir le maximum de rendement tout en courant le minimum de risque.

Dans le schéma ci-dessus, le point A (axe horizontal) représente le risque minimal que présente un portefeuille et son rendement espéré correspondant (axe vertical). L’application de formules mathématiques donne le pourcentage de chaque composante dans le portefeuille. La partie de la courbe qui va de A à B indique des portefeuilles optimaux dans lesquels un rendement plus élevé s’accompagne d’un risque plus élevé au fur et à mesure qu’on va vers B ; l’investisseur peut donc choisir, selon son niveau de tolérance au risque, le portefeuille qui lui convient le mieux. Tous les portefeuilles qui vont de A à B sont optimaux. À l’intérieur de la surface ABC, les portefeuilles courent un risque proportionnellement plus élevé sans générer de rendement optimal. Par exemple, au point C, on aura un grand risque accompagné d’un rendement très bas.

D’un point de vue objectif et rationnel, tout investisseur optera pour le segment AB, c’est-à-dire pour le portefeuille idéal qui présente le minimum de risque pour le niveau de rendement choisi.

La question qui se pose ici porte sur le niveau de risque que l’investisseur est capable d’assumer. C’est la question la plus difficile, parce que la réponse est subjective. En effet, le portefeuille idéal, même celui qui correspond au point A, pourrait présenter un risque plus grand que celui que l’investisseur est en mesure de supporter.

Comment mesure-t-on l’aversion au risque d’un investisseur ? Plusieurs méthodes qualitatives faisant appel à la psychologie suggèrent de déterminer quel est pour lui le risque le plus approprié, c’est-à-dire de décider combien investir en actions, en obligations et dans le marché monétaire. Certains tests aident à déterminer le profil psychologique de l’investisseur : il y a, entre autres, le PASS de W.G. Droms, le test de Baillard, Biehl & Kaiser – qui classe les investisseurs sur une échelle allant de « confiant » à « anxieux », et de « prudent » à « impétueux » –, celui de Barnewal, qui distingue les investisseurs passifs des investisseurs actifs, ou encore le test de Bonpian, qui compte huit types d’investisseur. La plus ancienne règle repose sur l’équation suivante : 100 – mon âge = le pourcentage à investir en actions, celles-ci étant estimées plus risquées que les obligations.

Une méthode quantitative et pratique est la suivante : on attribue à un investisseur un chiffre allant de 1 (aversion minimale au risque) à 5 (aversion maximale au risque). On donne ensuite au chiffre choisi la lettre A, qui représente ce qu’on appelle le « coefficient d’aversion au risque » (risk aversion coefficient).

Pour l’obtenir, on utilise la formule suivante (Utility formula^{note de bas de page 1}) : U = E(r) – 0,5 x A x σ².

Dans cette formule, U représente l’utilité, c’est-à-dire le score à attribuer à cet investissement dans un portefeuille donné en le comparant à un investissement sans risque, comme celui en bons du Trésor.

E(r) est le rendement espéré du portefeuille et σ2 (sigma au carré) est le carré de la volatilité (le carré du risque du portefeuille comme défini plus haut).

La partie de l’équation à la droite du signe « moins » indique le risque que présente la stratégie en soi en tenant compte aussi de l’aversion au risque de l’investisseur. Donc, la formule dans son ensemble nous donne la différence entre le rendement global espéré d’un titre (ou d’un portefeuille) et le risque couru. En effet, en soustrayant au rendement espéré E(r) le risque, il nous reste le rendement d’un investissement sans risque.

L’investisseur peut appliquer la formule à l’aide d’une simple calculatrice, ce qui lui permettra d’avoir une approche rationnelle dans le choix d’un titre pour son portefeuille.

Voici deux exemples de l’application de cette formule :

Exemple (i) :

• Taux d’intérêt sans risque (investissement en bons du Trésor) : 3 %
• Rendement espéré du portefeuille : 6 %
• Coefficient d’aversion au risque : 2
• Volatilité du rendement du titre : 16 %

En appliquant la formule, on obtient :

Score de l’utilité de l’investissement = 0,06 – 0,5 x 2 x 0,16² = 3,44 %

Ce résultat signifie qu’en soustrayant le risque du portefeuille (adapté à l’aversion au risque de l’investisseur) du résultat espéré, il reste un rendement sans risque supérieur à celui que généreraient des bons du Trésor (3 %). Donc, à risque égal, investir dans ce portefeuille est préférable à un investissement dans des bons du Trésor.

Exemple (ii) :

• Taux d’intérêt sans risque (investissement en bons du Trésor) : 3 %
• Rendement espéré du portefeuille : 6 %
• Coefficient d’aversion au risque : 3
• Volatilité du rendement du titre : 16 %

En appliquant la formule, on obtient :

Score de l’utilité de l’investissement = 0,06 – 0,5 x 3 x 0,16² = 2,16 %

Ce résultat signifie qu’en soustrayant le risque du portefeuille (adapté à l’aversion au risque de l’investisseur) du résultat espéré, il reste un rendement sans risque inférieur à celui des bons du Trésor (3 %). Donc, à risque égal, il est plus rentable d’investir dans des bons du Trésor que dans ce portefeuille.

Naturellement, le problème qui consiste à répondre à la question suivante persiste : sur une échelle de 1 à 5, quel chiffre (A) doit-on accorder à l’aversion au risque d’un investisseur ? En moyenne, on pourrait lui attribuer un A de 2,5.

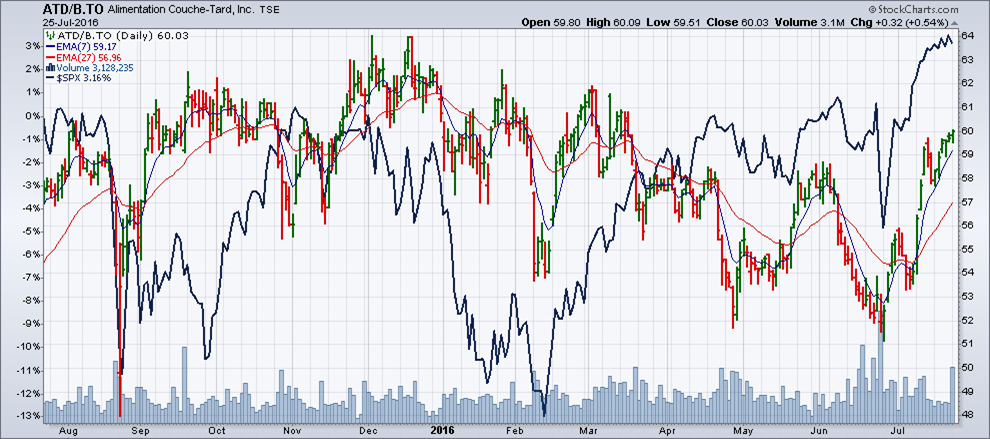
Si on applique cette formule à un investisseur dont A = 2,5 qui désire investir dans les actions de catégorie B de Couche-Tard (voir le graphique), on verrait, en appliquant la formule, si l’investisseur a raison ou pas de placer son argent dans ce titre. Voyons un peu.

Depuis 12 mois, ce titre a progressé de 3 % seulement (axe vertical de gauche). Sa volatilité historique, que l’on trouve sur le site de la Bourse de Montréal, est de 22,58 %, et le taux d’intérêt sans risque d’un an est de 0,51 %, selon la Banque du Canada.

On applique la formule^{note de bas de page 2} :

Score de l’utilité de l’investissement dans Couche-Tard : 0,03 – 0,5 x 2,5 x 0,2258² = – 0,0337 = – 3,37 %

À parité de risque pour l’investisseur dont A = 2,5, investir dans Couche-Tard est nettement plus risqué qu’investir dans des bons du Trésor qui ont une échéance d’un an (0,51 %).

Si l’aversion au risque est minime (A=1), Couche-Tard demeure moins avantageux comme investissement que les bons du Trésor d’un an, comme le montre le calcul suivant :

Score de l’utilité de l’investissement dans Couche-Tard : 0,03 – 0,5 x 1 x 0,2258² = 0,0045 = 0,45 %

Malgré l’engouement pour ce titre, on s’aperçoit que son rendement au cours des 12 derniers mois est bas. En émettant l’hypothèse que le rendement attendu de ce titre pour la prochaine année soit le même que celui des derniers 12 mois, même l’investisseur plus tolérant au risque devrait peut-être songer à éviter ce titre dans les conditions actuelles de rendement et de risque.