Le repas gratuit et le ratio de Sharpe
Pendant des décennies, au Canada comme aux États-Unis, les tavernes offraient un repas gratuit à leurs clients, le tout dans le but d'attirer la clientèle et d'augmenter leurs revenus. À l'époque, plusieurs organismes religieux s'étaient opposés à cette pratique la jugeant immorale. Ils avaient d'ailleurs lancé le slogan « Il n'y a pas de repas gratuit » (« There's no such thing as a free lunch ») puisqu'au final, le client paie son repas en dépensant davantage en consommations alcoolisées.
À la bourse, un repas faussement gratuit pourrait être comparé à une promesse de revenu facile. En existe-t-il ? Probablement. Par exemple, une émission privilégiée qui offre des rendements de 9 % par année représente assurément un risque élevé : la compagnie émettrice se lance dans des projets qui pourraient, en pratique, se révéler irréalisables, au moins à court terme. Il en résulte que la valeur de ces actions pourrait tomber bien en dessous du prix que l'investisseur avait payé.
L'américain William F. Sharpe, prix Nobel d'Économie 1990, est l'un des principaux créateurs de la théorie moderne de gestion de portefeuille. On lui doit, entre autres, le ratio qui porte son nom et qui mesure la performance d'un portefeuille. William F. Sharpe a contribué en 1964 à créer le modèle de gestion qui porte l'acronyme CAPM (Capital Asset Pricing Model), en français MEDAF (Modèle d'Équilibre des Actifs Financiers). Il s'agit d'un outil classique pour le calcul du rendement théoriquement requis d'un titre.
Tout investisseur devrait connaître le ratio de Sharpe : il est simple et fort utile parce qu'il établit la relation entre le rendement d'un titre et son risque. Ainsi, il permet de comparer le rendement avec le risque, une relation qui n'est pas toujours mise en évidence dans les investissements. Par exemple, on dira de tel fonds de placement que son rendement annuel moyen au cours des cinq dernières années a été de 12 %, mais on ne mentionnera pas quel est le risque dans lequel l'investisseur se retrouve avec ce fonds. La logique veut que plus grand est le rendement, plus grand devrait être le risque. Cependant, on pourrait en réalité se retrouver avec un investissement peu rentable par rapport à un grand risque.
En pensant construction et gestion d'un portefeuille de titres ou de FNB, les variables les plus connues sont donc le rendement et le risque. Alors que le rendement est intuitivement compréhensible, le risque est plus difficile à saisir. On l'appelle « écart-type » (ou volatilité) et il représente la turbulence des rendements sur une période donnée. Par exemple, dans le tableau 1, on a une série de 10 rendements annuels. Le portefeuille A montre un rendement annuel constant de 10 %, dont la volatilité est évidemment zéro. Le portefeuille B présente des variations importantes d'une année à l'autre : ici, la volatilité est de 24 %. À noter que le rendement moyen annuel des deux portefeuilles est le même. Malgré le fait que les deux rendements moyens annuels soient les mêmes, le portefeuille B fera en partie moins d'argent que le portefeuille A, comme le tableau le démontre. Dans ce cas-ci, une plus grande volatilité n'a pas été accompagnée d'un plus grand rendement.
L’effet dépressif de la volatilité
| Année | Portefeuille A | Portefeuille B | ||
|---|---|---|---|---|
| Rendement annuel | Valeur du portefeuille | Rendement annuel | Valeur du portefeuille | |
| Sans objet | Sans objet | 100 | Sans objet | 100 |
| 1 | 10 % | 110 | 30 % | 130 |
| 2 | 10 % | 121 | -20 % | 104 |
| 3 | 10 % | 133 | 51 % | 157 |
| 4 | 10 % | 146 | -12 % | 138 |
| 5 | 10 % | 161 | 27 % | 176 |
| 6 | 10 % | 177 | 15 % | 202 |
| 7 | 10 % | 195 | -7 % | 188 |
| 8 | 10 % | 214 | 1 % | 190 |
| 9 | 10 % | 236 | -17 % | 157 |
| 10 | 10 % | 259 | 32 % | 208 |
| Portefeuille A | Portefeuille B | |
|---|---|---|
| Rendement annuel moyen | 10 % | 10 % |
| Écart-type (volatilité) | 0 % | 24 % |
| Valeur du portefeuille après dix ans | 259 $ | 208 $ |
La définition de volatilité est quelque peu compliquée. Elle nous dit que le 2/3 des rendements individuels utilisés dans le calcul se trouve entre 10 % (la moyenne) ± 24 %, c'est-à-dire entre (+ 34 %) et (– 14 %). Plus grande est la volatilité et plus grandes sont les oscillations de rendement.
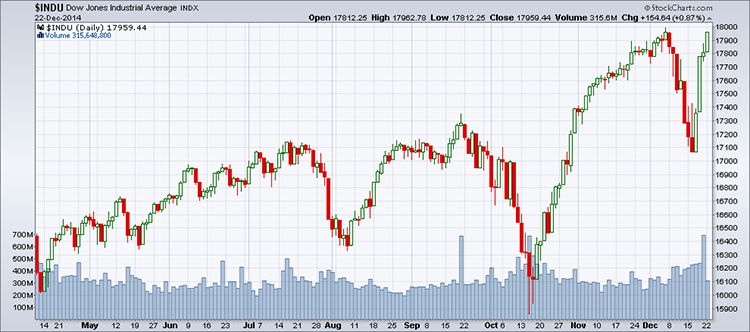
À titre d'exemple, un cas assez inusité de turbulence est celui qu'on a vécu en décembre 2014 (voir le graphique 1). L'indice Dow Jones des valeurs industrielles a chuté de 890 points en sept séances de bourse et a regagné 736 points dans les trois séances suivantes en revenant tout près de son record précédent, établit le 5 décembre. Entre la fin de septembre 2014 et le début de décembre, on a vécu un cas semblable, bien qu'étendu sur plusieurs séances.
La formule du ratio de Sharpe est la suivante : le rendement du portefeuille moins le rendement
des bons du Trésor. Le résultat est divisé par la volatilité du rendement du portefeuille.
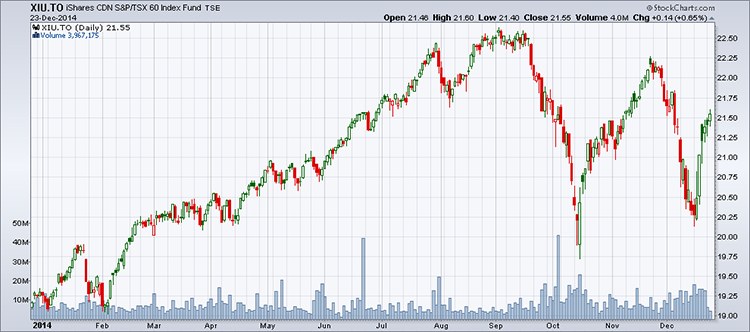
La volatilité annualisée du dernier mois est offerte par la Bourse de Montréal pour les titres canadiens pour lesquels il y a des options d'achat et de vente. Pour y accéder, l'investisseur doit se rendre sur le site de la Bourse. Ensuite, dans l'espace « Symbole », il écrit, par exemple, XIU. La page qui s'ouvre est celle qui montre les options d'achat et de vente. Au début de cette liste, on retrouve « Volatilité historique 30 jours ». Au moment d'écrire ces lignes, la volatilité du XIU.TO est 15,91 %.
Pour les titres américains, la volatilité est affichée dans le site www.cboe.com.
Pour appliquer le ratio de Sharpe au XIU.TO, en plus de la volatilité, on a donc besoin de connaître le rendement, par exemple sur un an, et le rendement des bons du Trésor.
La formule pour le calcul du rendement est la suivante : le prix final moins le prix initial plus les
dividendes. Le résultat est divisé par le prix initial.
Pour connaître le rendement du XIU sur un an (de décembre 2013 à décembre 2014) on doit connaître :
Prix au 24 décembre 2013 : 19,17 $
Prix au 23 décembre 2014 : 21,55 $
Dividendes sur an (approximativement): 0,50 $
Le rendement du XIU sur un an a été :
(21,55-19,17+0,50 $)/19,17 = 15,02 %
Pour connaitre le rendement des bons du Trésor, on visite le site de la Banque Centrale du Canada. On clique ensuite sur l'onglet « Statistiques », puis sur « Taux de rendement du marché monétaire ». Sur cette dernière page obtenue, on peut consulter la section « Bons du Trésor à 1 an ». Au moment d'écrire ces notes, le taux affiché est de 0,99 %.
On a à présent tous les éléments pour calculer le ratio de Sharpe selon la formule indiquée plus haut.
(15,02 %-0,99 %)/15,91 % = 0,88
Le ratio de Sharpe du marché canadien, symbolisé par le XIU.TO, basé sur les données historiques est donc 0,88. Ceci représente la référence. Pour juger si tout autre portefeuille « P » a été meilleur que celui représenté par le marché canadien, le ratio de Sharpe de « P » doit être plus élevé que celui du marché parce qu'il indique que la relation entre le risque et le rendement est plus avantageuse (moins de risque, plus de rendement).
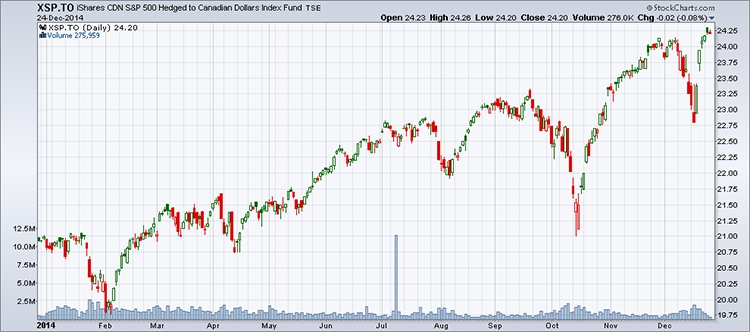
Prenons par exemple le XSP.TO, qui est le FNB de l'indice américain S&P500 offert au Canada en dollar canadien. Il est très intéressant parce que l'investisseur canadien n'a pas à se préoccuper du taux de change, dont le risque est assumé par l'émetteur de ce FNB (BlackRock).
La Bourse de Montréal nous indique que la volatilité de ce FNB est 13,53 %.
Le rendement, sur la même période de temps que le XIU.to, provient des données suivantes :
Prix au 27 décembre 2013 : 20,93 $
Prix au 24 décembre 2014 : 24,20 $
Dividendes sur an (approx.) : 0,35 $
En appliquant la formule des rendements vue plus haut, on obtiendra :
(24,20 $-20,93 $+0,35 $)/20,93 $ = 17,30 %
Le ratio de Sharpe du XSP.TO est donc :
(17,30 % - 0,99 %)/13,53 % = 1,21
Conclusion
Le ratio de Sharpe du XIU.TO est 0,88, alors que le ratio de Sharpe du XSP.TO est 1,21. La conclusion est qu'avoir investi en 2014 dans le XSP.TO a impliqué moins de risque (volatilité plus basse) avec un rendement supérieur qu'un l'investissement dans le XIU.TO.
L'investisseur a donc tout intérêt à inclure ce ratio dans ses critères de sélection de titres, de FNB, ou de fonds de placement pour avoir une vision plus rationnelle de la relation entre risque et rendement.
Nos exemples ont été ici illustrés à partir de données faciles à obtenir pour un investisseur, mais elles ne sont pas nécessairement celles qu'une institution financière (notamment la volatilité, les taux d'intérêt, les dividendes) pourrait utiliser. Le résultat, c'est-à-dire la comparaison entre deux ratios de Sharpe calculés avec la même méthode, est cependant une indication valable. Naturellement, le ratio de Sharpe peut changer avec les fluctuations du marché.
Les ratios de Sharpe sur FNB sont disponibles, à titre d'exemple, sur le site https://ca.finance.yahoo.com/ (symbole du FNB, suivi de « Risque »). Tout fonds de placement a aussi son ratio de Sharpe. Il suffit de le demander, pour ensuite le comparer avec celui du marché en général.
