La lunette de Galilée et l’approche de la cuillère

Le 12 mars 1610, Galileo Galilei (connu sous son nom français Galilée), savant et philosophe de la Renaissance italienne, publia un petit volume en latin dont le titre étrange était Sidereus Nuncius (Le messager céleste). Cet ouvrage portait un message révolutionnaire : Galilée affirmait avoir la preuve que la surface de la Lune n’était pas lisse, comme on l’avait cru pendant des siècles, mais qu’elle avait en fait un relief accidenté, comme la Terre. Il avait fait cette découverte en pointant vers la Lune sa lunette d’approche, une invention que Galilée avait améliorée au point d’obtenir un agrandissement des objets observés jusqu’à près de 9 fois. Un peu plus tard, toujours grâce à la lunette d’approche, il donna également la preuve que la Terre n’était pas au centre de l’Univers, mais qu’elle tournait autour du Soleil.

En finance, on a un outil très intéressant qui se compare à la lunette d’approche de Galilée, dans le sens où il nous donne une vision de la réalité des prix qu’on ne maitriserait pas aussi aisément sans lui. Il s’agit de l’écart-type (Standard Deviation en anglais).

L’écart-type est une mesure de la dispersion des données autour de leur moyenne. En prenant en considération les prix de fermeture d’un titre sur un mois de séances de bourse, on calcule le prix moyen. On détermine ensuite la différence entre chaque prix du mois et cette moyenne. On travaille mathématiquement ces données et on obtient l’écart-type, lequel nous avertit, par exemple, que deux tiers des prix du mois se trouvent à l’intérieur d’une certaine distance par rapport à la moyenne. Si on prend le prix moyen de 20 $ d’un titre X durant le mois avec un écart-type de 2 $, on dira que les deux tiers des prix utilisés pour déterminer la moyenne se trouvent à l’intérieur d’une fourchette de prix qui va de 22 $ (20 $+2 $) à 18 $ (20 $-2 $). Plus l’écart-type est grand et plus le titre est donc volatile. L’écart-type est une mesure obtenue à partir de données passées, mais on l’utilise pour avoir une idée approximative du possible mouvement de prix du titre de la prochaine séance.

Avant d’entrer dans un exemple plus concret, il convient de définir certains principes applicables lorsqu’il est question de statistiques. Selon la règle empirique, pour une distribution normale, la majorité des valeurs se situera dans un intervalle centré autour de la moyenne et dont les bornes se situent à 3 écarts-types de part et d'autre. Avec ce calcul, on conclut qu’environ 68,27 % des valeurs se situent à un écart-type de la moyenne.

On peut donc dire qu’il y a 68 % (pourcentage arrondi de 68,27 %) de probabilités que le mouvement de la prochaine période soit à l’intérieur d’une fourchette de prix déterminée. Cette fourchette est calculée à partir d’un certain nombre de mouvements de prix durant les périodes précédentes.

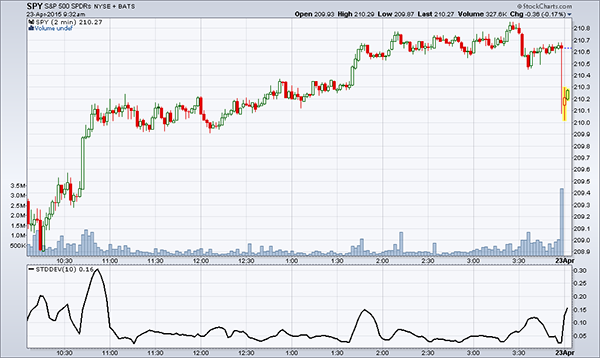
Dans le graphique 1, on présente le FNB américain SPY pour lequel chaque période illustrée est d’une durée de deux minutes. Dans l’ensemble, le graphique donne le portrait des mouvements du prix d’une seule séance de bourse.

Le graphique de l’écart-type se trouve dans la partie inférieure du graphique 1. Sur la gauche, il est indiqué « STDDEV (10) 0,16 ». Ceci signifie qu’il s’agit de l’écart-type (STDDEV), que le calcul fait par l’ordinateur a pris en considération les dix dernières périodes (10) et que l’écart-type est de 0,16 point. Cet écart-type est basé sur le comportement des 10 dernières périodes de 2 minutes chacune, au cours desquelles il y a 68 % de probabilités que le prix bouge à l’intérieur d’une fourchette de prix de 0,16 point. Si, par exemple, le prix du SPY est en ce moment à 210,00 points, il y a 68 % de probabilités que le prix varie à deux minutes entre 210,16 $ (210 + 0,16) et 109,84 $ (210 – 0,16). En d’autres mots, il y a 2 chances sur 3 (68 %) que le prix bouge à l’intérieur de cette fourchette et 1 chance sur 3 que le prix « sorte » de la fourchette.

Dans le graphique 1, l’écart-type est plutôt stable au cours de la journée, à l’exception du début de la séance jusqu’à 10h45, durant la séance à 13h45 et vers la fin de la séance, à 15h30. En moyenne, l’écart-type de cette séance est de 0,05 point, soit très moindre, ce qui indique un marché sans incertitudes.

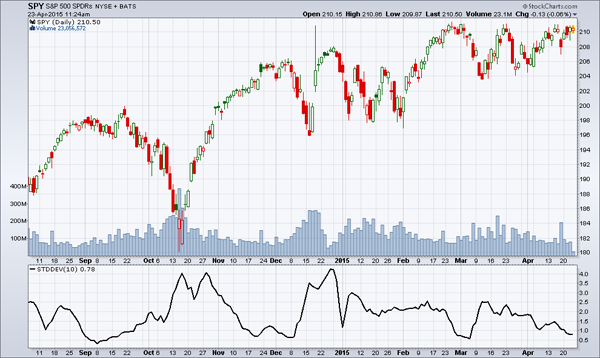
Le graphique 2 montre encore le SPY avec une période égale à une séance de bourse. On s’aperçoit ici que l’écart-type est plus grand : il est de 0,78 point le 23 avril 2015. Cependant, il se retrouve rarement à ce niveau et seulement pour de très courtes périodes sur la durée de vie du graphique. En moyenne, on pourrait dire que l’écart-type est 1,5 point sur la période donnée, soit 1,50 $ par action. Ce n’est pas beaucoup si on se limite à une action, mais si on en possède 1 000, la valeur globale peut varier, à 68 % de probabilités, de 1 500 $ par jour. Le graphique nous indique aussi qu’à partir de mars, l’écart-type diminue et il arrive le 23 avril à son plus bas niveau dans l’intervalle de temps du graphique. Il faut considérer l’écart-type comme une mesure de l’incertitude des investisseurs : on note qu’en avril les prix du SPY tendent à être moins nerveux et les fluctuations sont moins prononcées. Ceci indique que les prix semblent orientés vers une direction, la hausse dans le cas présent. L’écart-type témoigne de cette orientation du marché.

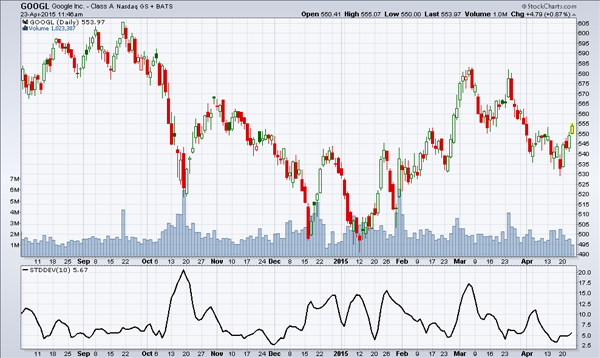
Naturellement, l’écart-type d’un titre dont le prix est plus élevé est aussi plus grand. Par exemple, dans Google, le graphique 3 montre un écart-type à la fin du graphique de 5,66 $, ce qui est en soi très élevé par rapport à celui des graphiques précédents. On note cependant aussi que le prix de Google est élevé. Pour mieux saisir la relation entre la valeur de l’écart-type et le prix du titre, il suffit de diviser le premier par le deuxième. Relativement au prix de Google (553,97 $) la fluctuation donnée par l’écart-type représente 1,02 % (5,66/553,97). Dans le cas du SPY, graphique 2, le ratio est par contre 0,37 % (0,78/ 210,50). Ce qui prouve que Google est définitivement plus risqué que l’indice américain S&P500 représenté par le SPY (en date du 23 avril 2015).

En conclusion, l’écart-type est une mesure utile pour déterminer en chiffres la valeur de la fluctuation d’un titre à la période suivante, avec 68 % de probabilité d’avoir raison.

Une des applications de cette mesure se retrouve dans la « méthode de la cuillère » (Teaspoon Approach), l’une de mes méthodes dans la négociation active : on entre dans le marché à un signal d’analyse technique et on place tout de suite un ordre de sortie à un prix qui est à l’intérieur de la fourchette de l’écart-type. En principe, on a 68 % de chances de voir notre ordre de sortie réalisé. Potentiellement, on gagne moins à chaque transaction, mais on profite d’une plus grande tranquillité d’esprit.

En effet, en suivant cette méthode, on prend une seule décision basée sur l’analyse technique, parce que la sortie est en fonction de la probabilité élevée d’avoir un gain, peu importe l’ordre de grandeur : on obtient donc une cuillérée d’argent, petite, mais fréquente.